Rekurzió

Rekurzió az, amikor egy eljárás vagy függvény - közvetve vagy közvetlenül - önmagát hívja. A végtelen rekurzió elkerülésére szükségünk van egy feltételre, amely valamilyen lépésszám után leállítja a rekurziót.
A matematikában találkozhatunk rekurzív definíciókkal, ilyen például a faktoriális kiszámítása (a faktoriális jele: !)
n! (olvasd: n faktoriális):=2·3·...·(n-1)·n
pl. 0! (nulla faktoriális) értéke 1
n! pedig n*(n-1)!. Tehát egy szám faktoriálisát úgy számíthatjuk ki, hogy kiszámítjuk a nála eggyel kisebb szám faktoriálisát és megszorozzuk a számmal. A rekurzió véget ér, ha eljutunk a 0-hoz.

Ez a definíció rekurzív formára is átírható:

Így tehát az 5!-t visszavezetjük 5·4!-ra, vagyis 4!-ra, azt 3!-ra stb..., míg végül elérkezünk 0!-hoz, amit már nem vezetünk vissza. A legtöbb rekurzív utasítás tartalmaz egy leállási feltételt, ez akadályozza meg a végtelen rekurziót. A fenti függvény megvalósítása VB.NET-ben

Function Fakt(ByVal n As Integer) As Integer

        If n = 0 Then
            Fakt = 1
        Else
            Fakt = n * Fakt(n - 1) 'Rekurzív hívás: saját magát hívja a függvény
        End If

    End Function

Látható, hogy a matematikai definíció szinte egy az egyben átírható volt Basicre. Ennek az az oka, hogy a Basic eljáráskezelése fel van készülve a rekurzióra: eljáráshíváskor a Basic elmenti a verembe a globális, hívott eljárásban is szereplő változókat, majd az eljárás lefutása után az eljárás lokális változói megszűnnek, és a veremből előkerülnek a globális változók. Ha végigkövetjük a függvény működését, kiderül, hogy voltaképpen az n·(n-1)·...·2·1·1 szorzást végzi el, amit akár ciklussal is megoldhattunk volna. A ciklus előnye a rekurzív megoldáshoz képest, hogy a veremigénye (és olykor az időigénye is) kisebb. A rekurzív megoldások viszont sokszor érthetőbbek és áttekinthetőbbek.

A Fibonacci-számok a matematikában az egyik legismertebb rekurzív sorozat elemei. Az első két eleme 0 és 1, a további elemeket az előző kettő összegeként kapjuk. Képletben

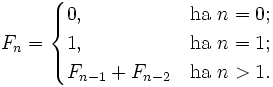
: $F_n= \begin{cases} 0, & \mbox{ha }n=0; \\ 1, & \mbox{ha }n=1; \\ F_{n-1}+F_{n-2} & \mbox{ha }n>1. \end{cases}$

A sorozatot nyugaton 1202-ben Fibonacci találta meg, aki Liber Abaci (Könyv az abakuszról) című művében egy képzeletbeli nyúlcsalád növekedését adta fel gyakorlófeladatként: hány pár nyúl lesz n hónap múlva, ha feltételezzük, hogy

az első hónapban csak egyetlen újszülött nyúl-pár van;
az újszülött nyúl-párok két hónap alatt válnak termékennyé;
minden termékeny nyúl-pár minden hónapban egy újabb párt szül;
és a nyulak örökké élnek?
Az első néhány Fibonacci szám: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352...

Feladat: Írjuk meg a Fib(n) függvényt rekurzív

Function fib(ByVal n)
        If n < 2 Then
            Return n
        Else
            Return fib(n - 1) + fib(n - 2)
        End If
End Function

és nem rekurzív (ciklusos) módon is!

Private Sub fibo()
        Dim fibonacci(10) As Long
        Dim I As Integer
        fibonacci(1) = 1
        fibonacci(2) = 1
        For I = 3 To 10
            fibonacci(I) = fibonacci(I - 1) + fibonacci(I - 2)
        Next I
        For I = 1 To 10
            MsgBox("Fibonacci" & CStr(I) & ":= " & CStr(fibonacci(I)))
        Next I
    End Sub

feladat: vezesd vissza a szorzást rekurzív összeadásra! a·n=a+a·(n-1), és a·n=0 ha n=0 vagy a=0