Ciklusok
Ciklusok
Számlálóvezérelt ciklus
for i=0 to 15 Step 3
utasítások
Exit for 'itt
kiléphetsz a ciklusból, ha nagyon muszáj
utasítások
Next
Private Sub ciklus()
Dim i As Integer
For i = 0 To 15 Step 3
MsgBox(i)
Next
End Sub
for i=10 to 1 Step -1
' léptetés visszafelé (jól
jöhet a buborékrendezésnél)
utasítások
Exit for
utasítások
Next
Elöltesztelős ciklus mindaddig ismétli
az utasításokat, amíg a feltétel kiértékelése igaz
Do While|Until feltétel
utasítások
Exit Do
utasítások
Loop
Hátultesztelős ciklus azaz előbb
lefuttatja az utasításokat, majd utána értékeli ki a feltételt.
Lévén, hogy a do-while (Pascalban repeat until) hátul tesztelős, ezért egyszer
tuti lefut.
Do
utasítások
Exit Do
utasítások
Loop While|Until feltétel
Mint látható, mind az előltesztelős,
mind hátultesztelős ciklus esetében választhatunk, hogy a feltétel a
ciklusbanmaradás vagy a ciklus befejezésének feltétele legyen. (While illetve
Until kulcsszótól függően)
For
Each
For Each elem In csoport
utasítások
Exit For
utasítások
Next
Egy csoport (Collection) elemein
lépked végig ez a ciklus
Példa:
Public Class Form1
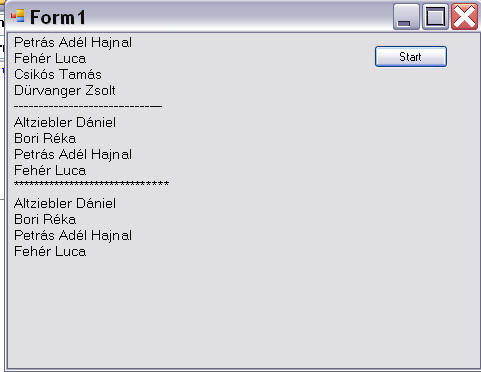
Dim Forrás() As String = {"Altziebler Dániel", "Bori Réka", "Petrás Adél Hajnal", "Fehér Luca", "Csikós Tamás", "Dürvanger Zsolt", "Vad Csaba"}
Dim gr As Graphics = Me.CreateGraphics
Dim Betu_Méret As Integer = 14
Dim Betu_Típus As New Font("Ariel", Betu_Méret, FontStyle.Regular, GraphicsUnit.World)
Dim Nyomtatandó_Sorok_Száma As Integer = 0
Dim prn_sor As String
Private Sub Kiírat_2_5()
Dim I, J As Integer
Dim SpTomb() As String
Dim Knev As String = ""
For I = 2 To 5
SpTomb = Split(Forrás(I), " ")
prn_sor = ""
For J = 0 To UBound(SpTomb)
prn_sor = prn_sor & SpTomb(J) & " "
Next
gr.DrawString(prn_sor, Betu_Típus, Brushes.Black, 4, Nyomtatandó_Sorok_Száma)
Nyomtatandó_Sorok_Száma = Nyomtatandó_Sorok_Száma + Betu_Méret + 2
Next
End Sub
Private Sub KiíratLucáig()
Dim I, J As Integer
Dim SpTomb()
Dim Knev As String = ""
I = 0
Do Until Knev = "Luca" 'elöl tesztel
SpTomb = Split(Forrás(I), " ")
Knev = SpTomb(1)
I = I + 1
prn_sor = ""
For J = 0 To UBound(SpTomb)
prn_sor = prn_sor & SpTomb(J) & " "
Next
gr.DrawString(prn_sor, Betu_Típus, Brushes.Black, 4, Nyomtatandó_Sorok_Száma)
Nyomtatandó_Sorok_Száma = Nyomtatandó_Sorok_Száma + Betu_Méret + 2
Loop
End Sub
Private Sub KiíratLucáig_2() 'hátul
tesztelős
Dim I, J As Integer
Dim SpTomb()
Dim Knev As String = ""
I = 0
Do
SpTomb = Split(Forrás(I), " ")
Knev = SpTomb(1)
I = I + 1
prn_sor = ""
For J = 0 To UBound(SpTomb)
prn_sor = prn_sor & SpTomb(J) & " "
Next
gr.DrawString(prn_sor, Betu_Típus, Brushes.Black, 4, Nyomtatandó_Sorok_Száma)
Nyomtatandó_Sorok_Száma = Nyomtatandó_Sorok_Száma + Betu_Méret + 2
Loop While Knev <> "Luca"
End Sub
Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click
Call Kiírat_2_5()
prn_sor = "------------------------------"
gr.DrawString(prn_sor, Betu_Típus, Brushes.Black, 4, Nyomtatandó_Sorok_Száma)
Nyomtatandó_Sorok_Száma = Nyomtatandó_Sorok_Száma + Betu_Méret + 2
Call KiíratLucáig()
prn_sor = "******************************"
gr.DrawString(prn_sor, Betu_Típus, Brushes.Black, 4, Nyomtatandó_Sorok_Száma)
Nyomtatandó_Sorok_Száma = Nyomtatandó_Sorok_Száma + Betu_Méret + 2
Call KiíratLucáig_2()
End Sub
End Class
Feladat:
Döntsük el egy adott természetes számról, hogy prím-e!
A feladatra többféle megoldás adható. Egy lehetséges út, hogy az osztók számát
meghatározzuk, és ha pontosan két osztója van, akkor a szám prím. Ez a megoldás
azonban nagy számok vizsgálatánál nem szerencsés. Ha ugyanis például 2007-ről
akarjuk eldönteni, hogy
prím-e, már az pár lépésben kiderül, hogy a 3 osztója, a így további vizsgálat
tehát fölösleges. A fentiek alapján adódik a megoldás: végezzük a
vizsgálatot 2-től kezdve az első osztóig! Prímszámok esetén ez maga a szám,
összetett számok estén viszont az első prímosztó, tehát ekkor az algoritmus
lényegesen gyorsabb
Az eljárás tehát a következő. Legyen kezdetben I értéke 2. Ha I nem osztója
vizsgált számnak, akkor vegyük a kővetkező számot I+1, és vizsgáljuk azt:
Eljárás Prímvizsgálat
Be: n
I=2
Ciklus amíg I nem osztója n-nek
I=I+1
ciklus vége
Ha I= n akkor Ki:“Prím”
Ha I > n akkor Ki:“Összetett”
Eljárás vége
A fenti eljárásban új elem a Ciklus amíg szerkezet. Ezúttal a ciklus nem egy
számsoron (I = l-től n-ig) Fut végig, hanem a ciklusmagban lévő utasítást addig
ismétli csak, amíg az adott feltétel teljesül. Ez a szerkezet általánosabb,
Írj eljárást, amely egy számról eldönt, hogy
prímszám-e?

